1199번: 오일러 회로
첫 줄에는 정점의 수 N(1 ≤ N ≤ 1,000)이 주어진다. 그리고 다음 N개의 줄에 대해 인접행렬의 정보가 주어진다. i+1번째 줄에는 i번 정점에 대한 인접행렬이 주어진다. 두 정점 사이에 간선이 여러
www.acmicpc.net
오일러 회로라는 것은, 그래프 상에 존재하는 모든 간선들을 오로지 단 한번만 방문해서 출발지로 되돌아오는 경로를 오일러 회로 또는 오일러 경로라고 부른다
시작점과 도착점이 같으면 오일러 회로, 시작점과 도착점이 다르면 오일러 경로라고 부른다.
- 무향 그래프 일때
1) 오일러 경로가 존재할 조건은, 시작점과 도착점이 달라야 하고, 차수가 홀수인 정점이 2개 있어야한다. (차수가 홀수인 두 정점이 시작점과 도착점이 된다)
2) 오일러 회로가 존재할 조건은, 시작점과 도착점이 같아야 하고, 차수가 홀수인 정점이 없어야 한다.
- 유향 그래프 일때
1) 오일러 경로가 존재할 조건은, indegree 가 1 적은 정점 하나가 시작점이고, outdegree 가 1적은 정점 하나가 끝점으로 정해진다 indegree 와 outdegree 가 불일치하는 정점이 이 둘말고는 없어야 한다.
2) 오일러 회로가 존재하려면, 모든 정점에 대해서 indegree 와 outdegree 가 같아야 한다.
(시작점과 끝점을 빼고는 들어오는 간선이 있으면 반드시 나가는 간선이 있어야 하기 때문이다)
오일러 회로를 탐색하는 대표적인 알고리즘은
Hierholzer's Algorithm 라는 알고리즘으로, 이 알고리즘의 진행과정은 아래와 같이 요약된다.
1. 그래프 내에서 임의의 정점 v 를 뽑고, v 에서 출발해서 v 로 돌아오는 경로를 하나 찾는다
2. 1번에서 찾아낸 경로에 속한 정점 중 인접한 경로를 쓰지 않는 정점이 있다면 그 정점을 기준으로 다시 1번의 과정을 반복한다.
- 참고 : blog.naver.com/kks227/220800097205
오일러 경로(Eulerian Path), 오일러 회로(Eulerian Circuit) (수정: 2019-08-20)
이번에 소개할 내용은 오일러 경로(Eulerian trail) 및 오일러 회로(Eulerian circuit)입니다.위상수학, ...
blog.naver.com
그림으로 예제를 나타내면 아래와 같다
1. 먼저 정점 A 를 기준으로 A에서 출발해서 다시 A 로 돌아오는 경로 A -> B -> C -> D -> A 를 잡는다.
[A, B, C, D, A]
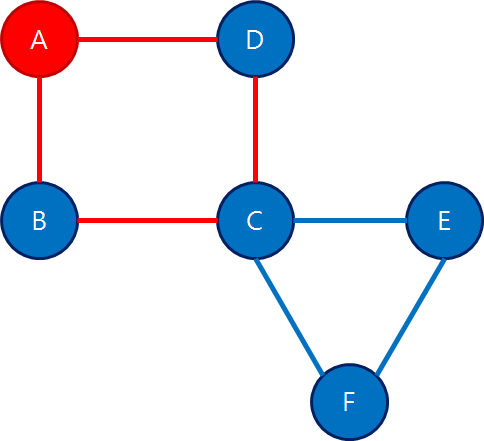
2. 그 다음으로 위의 경로 [A, B, C, D, A] 에 속하는 정점 중 인접한 간선을 사용하지 않은 정점이 딱하나 있는데 정점 C 가 이에 해당하고, 정점 C 를 기반으로 C 에서 출발해서 C 로 되돌아오는 경로를 찾아낸다.
새로 찾아낸 경로가 [C, E, F, C] 가 되며, 기존의 경로 [A, B, C, D, A] 에서 C 를 새 경로 값으로 바꾼다
[A, B, C, E, F, C, D, A]

위 예제에서는 [A, B, C, E, F, C, D, A] 가 끝이지만 만약 또 다른 정점이 있고 그 정점을 기준으로 1의 과정을 반복 할 수 있다면 찾아놓은 경로 값에 재귀적으로 새 경로를 추가해주면 된다.
말은 이렇게 쉽게 말하긴 했는데, 구현자체가 쉽지도 않고, 응용 문제도 잘 나오지 않는다고 한다.
- C++
|
#include <iostream>
#define MAX 1001
using namespace std;
int N;
int adj[MAX][MAX]; // 그래프
int degree[MAX]; // 차수
void dfs(int node) {
for (int i = 1; i <= N; ++i) {
while(adj[node][i]) {
adj[node][i]--;
adj[i][node]--;
dfs(i);
}
}
cout << node << " ";
}
int main() {
cin.tie(0); ios_base::sync_with_stdio(0);
cin >> N;
for (int i = 1; i <= N; ++i) {
for (int j = 1; j <= N; ++j) {
cin >> adj[i][j];
degree[i] += adj[i][j]; // 양방향 그래프이므로 둘다 +
degree[j] += adj[i][j];
}
}
bool isEuler = true;
for (int i = 1; i <= N; ++i) {
degree[i] /= 2; // 양방향 간선
if (degree[i] % 2) { // 홀수인게 하나라도 있으면 안됨
isEuler = false;
break;
}
}
if (isEuler) {
dfs(1);
} else {
cout << "-1";
}
return 0;
}
|
cs |

'PS' 카테고리의 다른 글
| BOJ 7579 - 앱 (0) | 2021.03.10 |
|---|---|
| BOJ 1943 - 동전 분배 (0) | 2021.03.09 |
| BOJ 2513 - 통학버스 (0) | 2021.03.04 |
| BOJ 1577 - 도로의 갯수 (0) | 2021.03.03 |
| BOJ 2109 - 순회강연 (0) | 2021.03.02 |
